![[algorithm] 정렬(버블정렬, 선택정렬, 삽입정렬, 퀵정렬, 병합정렬, 힙정렬, 기수정렬, 계수정렬)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fch3UxT%2FbtsHqK8KMya%2FAAAAAAAAAAAAAAAAAAAAAHjuahHGqIphZD-7oJOUBj5YuP1FgUqGSMJjhH6M-UkB%2Fimg.gif%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DFdCIp2%252BFIcgDSuvwMPZO3KK4g5A%253D)

[algorithm] 정렬(버블정렬, 선택정렬, 삽입정렬, 퀵정렬, 병합정렬, 힙정렬, 기수정렬, 계수정렬)CS/CS2024. 5. 15. 21:48
Table of Contents
정렬
버블 정렬(Bubble Sort) - 시 O(n^2) | 공 O(n)
서로 인접한 두 원소의 대소를 비교, 조건이 맞지 않다면 자리를 교환해 정렬
- 선택정렬(Selection Sort)과 유사
- 배열의 길이가 길어질수록 비효율적
- 시간 복잡도 계산
- (n-1) + (n-2) + (n-3) + … + 2 + 1 => n(n-1)/2
- 최선, 평균, 최악의 경우 모두 시간복잡도가 O(n^2) 으로 동일
- 공간 복잡도 : O(n)

void bubbleSort(int[] arr) {
int temp = 0;
for(int i = 0; i < arr.length; i++) { // 1.
for(int j= 1 ; j < arr.length-i; j++) { // 2.
if(arr[j-1] > arr[j]) { // 3.
// swap(arr[j-1], arr[j])
temp = arr[j-1];
arr[j-1] = arr[j];
arr[j] = temp;
}
}
}
System.out.println(Arrays.toString(arr));
}
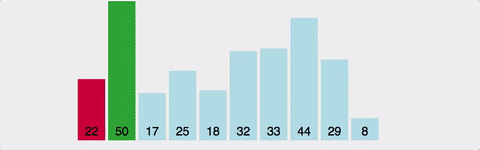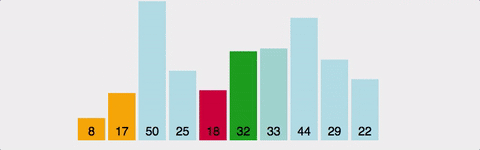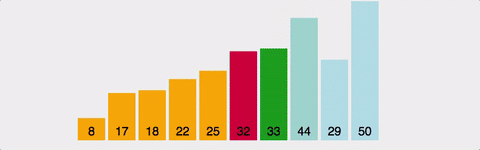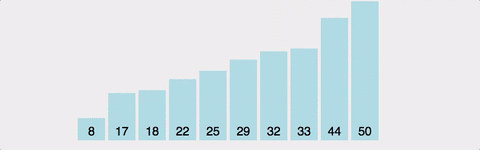
선택 정렬(Selection Sort) - 시 O(n^2) | 공 O(n)
해당 순서에 원소를 넣을 위치는 이미 정해져 있고, 어떤 원소를 넣을지 선택하는 알고리즘
- 버블 정렬과 유사하지만 조금 더 빠름.
- 정렬을 위한 비교 횟수는 많음.
- Bubble Sort에 비해 실제로 교환하는 횟수는 적기 때문에 많은 교환이 일어나야 하는 자료상태에서 비교적 효율적임.
- 배열의 길이가 길어질수록 비효율적
- 시간 복잡도 계산
- (n-1) + (n-2) + … + 2 + 1 => n(n-1)/2
- 최선, 평균, 최악의 경우 시간복잡도는 O(n^2)
- 공간 복잡도 : O(n)
void selectionSort(int[] arr) {
int indexMin, temp;
for (int i = 0; i < arr.length-1; i++) { // 1.
indexMin = i;
for (int j = i + 1; j < arr.length; j++) { // 2.
if (arr[j] < arr[indexMin]) { // 3.
indexMin = j;
}
}
// 4. swap(arr[indexMin], arr[i])
temp = arr[indexMin];
arr[indexMin] = arr[i];
arr[i] = temp;
}
System.out.println(Arrays.toString(arr));
}
삽입 정렬(Insertion Sort) - 시 O(N)~O(n^2) | 공 O(n)
2번째 원소부터 시작하여 그 앞(왼쪽)의 원소들과 비교하여 삽입할 위치를 지정한 후, 원소를 뒤로 옮기고 지정된 자리에 자료를 삽입
- 선택 정렬과 유사하지만, 조금 더 효율적임
- 배열의 길이가 길어질수록 비효율적
- 시간 복잡도 계산
- (n-1) + (n-2) + … + 2 + 1 => n(n-1)/2
- 최선 - O(n) , 평균&최악 - O(n^2)
- 공간 복잡도 : O(n)

void insertionSort(int[] arr)
{
for(int index = 1 ; index < arr.length ; index++){ // 1.
int temp = arr[index];
int prev = index - 1;
while( (prev >= 0) && (arr[prev] > temp) ) { // 2.
arr[prev+1] = arr[prev];
prev--;
}
arr[prev + 1] = temp; // 3.
}
System.out.println(Arrays.toString(arr));
}
퀵 정렬(Quick Sort) - 시 O(nlog₂n)~ O(n^2) | 공 O(n)
분할 정복(divide and conquer) 방법 을 통해 주어진 배열을 정렬(JAVA Arrays.sort() : 퀵 정렬 알고리즘)
`*`[분할 정복(divide and conquer) 방법]
문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략
- 빠른정렬로 분류되며, 병합 정렬과 함께 많이 언급됨
- 정렬하고자 하는 배열이 오름차순 정렬되어있거나 내림차순 정렬되어있으면 O(n^2)의 시간복잡도를 가짐(수행시간이 매우 길어짐)
- 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라, 한 번 결정된 피벗들이 추후 연산에서 제외됨
- 다른 정렬 알고리즘과 비교했을 때도 가장 빠름
- 시간 복잡도 계산
- 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산
- 최선 : log₂n * n = nlog₂n / 최악 : n * n = n^2
- 공간 복잡도 : O(n)



- 정복(conquer)
public void quickSort(int[] array, int left, int right) {
if(left >= right) return;
// 분할
int pivot = partition();
// 피벗은 제외한 2개의 부분 배열을 대상으로 순환 호출
quickSort(array, left, pivot-1); // 정복(Conquer)
quickSort(array, pivot+1, right); // 정복(Conquer)
}
- 분할(Divide)
public int partition(int[] array, int left, int right) {
/**
// 최악의 경우, 개선 방법
int mid = (left + right) / 2;
swap(array, left, mid);
*/
int pivot = array[left]; // 가장 왼쪽값을 피벗으로 설정
int i = left, j = right;
while(i < j) {
while(pivot < array[j]) {
j--;
}
while(i < j && pivot >= array[i]){
i++;
}
swap(array, i, j);
}
array[left] = array[i];
array[i] = pivot;
return i;
}
병합(합병) 정렬(Merge Sort) - 시 O(nlogn) | 공 O(1)
요소를 쪼갠 후, 다시 합병시키면서 정렬해나가는 방식
- 분할 및 정복 방법으로 구현(모든 숫자를 독립적으로 분할)
- 빠른정렬로 분류되며, 퀵 정렬과 함께 많이 언급됨
- 퀵정렬과의 차이점
- 퀵정렬 : 우선 피벗을 통해 정렬(partition) → 영역을 쪼갬(quickSort)
- 합병정렬 : 영역을 쪼갤 수 있을 만큼 쪼갬(mergeSort) → 정렬(merge)
- 합병의 대상이 되는 두 영역이 각 영역에 대해서 정렬이 되어있기 때문에, 단순히 두 배열을 순차적으로 비교하면서 정렬할 수가 있음
- LinkedList를 퀵정렬을 통해 정렬하면 성능이 좋지 않음 -> 병합정렬 사용
- 퀵정렬의 경우, 순차 접근이 아닌 임의 접근이기 때문
- 따라서, 오버헤드 발생이 증가하게 됨

- mergeSort
public void mergeSort(int[] array, int left, int right) {
if(left < right) {
int mid = (left + right) / 2;
mergeSort(array, left, mid);
mergeSort(array, mid+1, right);
merge(array, left, mid, right);
}
}
- merge()
public static void merge(int[] array, int left, int mid, int right) {
int[] L = Arrays.copyOfRange(array, left, mid + 1);
int[] R = Arrays.copyOfRange(array, mid + 1, right + 1);
int i = 0, j = 0, k = left;
int ll = L.length, rl = R.length;
while(i < ll && j < rl) {
if(L[i] <= R[j]) {
array[k] = L[i++];
}
else {
array[k] = R[j++];
}
k++;
}
// remain
while(i < ll) {
array[k++] = L[i++];
}
while(j < rl) {
array[k++] = R[j++];
}
}
힙 정렬(Heap Sort) - 시 O(nlogn) |
완전 이진 트리를 기본으로 하는 힙(Heap) 자료구조를 기반으로 한 정렬 방식
* 완전 이진 트리 : 삽입 할 때 왼쪽부터 차례대로 추가하는 이진 트리
- 유용 할 때 :
- 가장 크거나 가장 작은 값을 구할 때 유리
- 최소 힙 또는 최대 힙의 루트 값이기 떄문에 한번의 힙 구성을 통해서 구하는 것이 가능
- 최대 k만큼 떨어진 요소들을 정렬할 때
- 삽입 정렬보다 더욱 개선된 결과
- 가장 크거나 가장 작은 값을 구할 때 유리
- 퀵정렬과 합병정렬의 성능이 좋기 때문에 힙 정렬의 사용빈도가 높지는 않음.

public class Heap
{
private int[] element; //element[0] contains length
private static final int ROOTLOC = 1;
private static final int DEFAULT = 10;
public Heap(int size) {
if(size>DEFAULT) {element = new int[size+1]; element[0] = 0;}
else {element = new int[DEFAULT+1]; element[0] = 0;}
}
public void add(int newnum) {
if(element.length <= element[0] + 1) {
int[] elementTemp = new int[element[0]*2];
for(int x = 0; x < element[0]; x++) {
elementTemp[x] = element[x];
}
element = elementTemp;
}
element[++element[0]] = newnum;
upheap();
}
public int extractRoot() {
int extracted = element[1];
element[1] = element[element[0]--];
downheap();
return extracted;
}
public void upheap() {
int locmark = element[0];
while(locmark > 1 && element[locmark/2] > element[locmark]) {
swap(locmark/2, locmark);
locmark /= 2;
}
}
public void downheap() {
int locmark = 1;
while(locmark * 2 <= element[0])
{
if(locmark * 2 + 1 <= element[0]) {
int small = smaller(locmark*2, locmark*2+1);
if(element[small] >= element[locmark]) break;
swap(locmark,small);
locmark = small;
}
else {
if(element[locmark * 2] >= element[locmark]) break;
swap(locmark, locmark * 2);
locmark *= 2;
}
}
}
public void swap(int a, int b) {
int temp = element[a];
element[a] = element[b];
element[b] = temp;
}
public int smaller(int a, int b) {
return element[a] < element[b] ? a : b;
}
}
기수 정렬(Radix Sort) - 시 O(w * (k+n)) |
기수별로 비교 없이 수행하는 정렬 알고리즘
- 정수같은 자료형에 있어서 정렬 속도가 매우 빠르다.
- 데이터 전체 크기에 기수 테이블의 크기만한 메모리가 더 필요함
- 입력 데이터의 최대값에 따라서 Counting Sort의 비효율성을 개선하기 위해서, Radix Sort를 사용할 수 있음(입력 데이터의 최대값이 작으면 Good)
- 장점 : 문자열, 정수 정렬 가능
- 단점 : 자릿수가 없는 것은 정렬할 수 없음. (부동 소숫점)
- 시간 복잡도 계산
- O(w * (k+n)) : 여기서 w는 기수의 크기, k는 기수의 도메인 크기 즉 O(n)

void countSort(int arr[], int n, int exp) {
int buffer[n];
int i, count[10] = {0};
// exp의 자릿수에 해당하는 count 증가
for (i = 0; i < n; i++){
count[(arr[i] / exp) % 10]++;
}
// 누적합 구하기
for (i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
// 일반적인 Counting sort 과정
for (i = n - 1; i >= 0; i--) {
buffer[count[(arr[i]/exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
for (i = 0; i < n; i++){
arr[i] = buffer[i];
}
}
void radixsort(int arr[], int n) {
// 최댓값 자리만큼 돌기
int m = getMax(arr, n);
// 최댓값을 나눴을 때, 0이 나오면 모든 숫자가 exp의 아래
for (int exp = 1; m / exp > 0; exp *= 10) {
countSort(arr, n, exp);
}
}
int main() {
int arr[] = {170, 45, 75, 90, 802, 24, 2, 66};
int n = sizeof(arr) / sizeof(arr[0]); // 좋은 습관
radixsort(arr, n);
for (int i = 0; i < n; i++){
cout << arr[i] << " ";
}
return 0;
}
계수 정렬(Counting Sort)
- 정렬 과정
- 가장 작은 데이터부터 가장 큰 데이터까지의 범위가 모두 담길 수 있는 리스트를 생성
- 데이터를 하나씩 확인하며 데이터의 값과 동일한 인덱스의 데이터를 1씩 증가
- 증가된 리스트에서 0인 값을 제외하고, 인덱스를 인덱스 값만큼 출력

'CS > CS' 카테고리의 다른 글
| 데이터베이스-동시성 제어 (0) | 2024.02.06 |
|---|---|
| [DB] 트렌젝션과 ACID (0) | 2024.01.30 |
| [DB] Index란? (0) | 2024.01.18 |
| [CS] 엣지 케이스와 코너 케이스는 뭘까?(feat.. 조금 더 안정성 있는 서비스를 향하여..) (0) | 2024.01.16 |
| www.google.com을 주소창에 쳤을 때 화면이 나오기까지의 과정 (0) | 2024.01.01 |

@Yanako :: Yana's coding story였는데요, 우당탕탕 개발일지가 맞는것같
야나의 코딩 일기장 :) #코딩블로그 #기술블로그 #코딩 #조금씩,꾸준히
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
